Linear Discriminant Analysis / Fisher’s Linear Discriminant

Type
Linear Classifier

Good Illustration: An illustrative introduction to Fisher’s Linear Discriminant - Thalles’ blog

Find an orientation along which the projected samples are well separated.

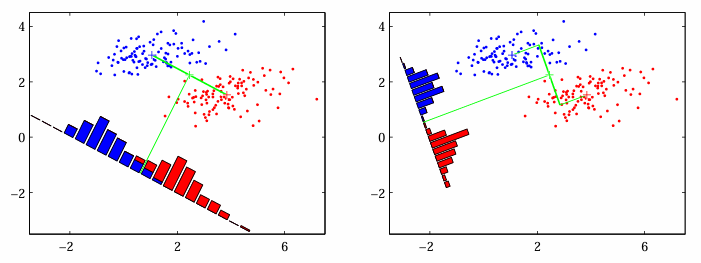
Fisher’s Linear Discriminant

  • We want class means to be as far as possible. The denominator is the total within-class scatter of the projected samples.

arg⁡max⁡w∣m+−m−∣2s+2+s−2\arg\max_{w} \frac{\vert m_{+} - m_{-} \vert ^2}{s_{+}^2 + s_{-}^2}

where $s_+^2$ or $s_-^2$ is (almost like variance),

s+2=∑x∈C+(wTx−m+)2s_{+}^2 = \sum_{x \in C_{+}} (w^T x - m_{+})^2

m+=1N+∑x∈C+wTx=wTm+m_+ = \frac{1}{N_+} \sum_{x \in C_+} \mathbf{w}^T \mathbf{x} = \mathbf{w}^T \mathbf{m}_+

Define following matrices:

S+=∑x∈C+(x−m+)(x−m+)TS_+ = \sum_{x \in C_+} (\mathbf{x} - \mathbf{m}_+)(\mathbf{x} - \mathbf{m}_+)^T

SW=S++S−S_W = S_+ + S_-

$S_+$ or $S_-$ takes the form

[var(x1)cov(x1,x2)cov(x1,x2)var(x2)]\begin{bmatrix} var(x_1) && cov(x_1,x_2) \\ cov(x_1,x_2) && var(x_2) \end{bmatrix}

SB=(m+−m−)(m+−m−)TS_B = (m_+-m_-)(m_+-m_-)^T

Using these we obtain,

J(w)=∣m+−m−∣2s+2+s−2=wTSBwwTSWwJ(\mathbf{w}) = \frac{\vert m_+ - m_- \vert ^2}{s_+^2 + s_-^2} = \frac{\mathbf{w}^T S_B \mathbf{w}}{\mathbf{w}^T S_W \mathbf{w}}

$J$ is maximized when (take derivate with respect to w)

(wTSBw)SWw=(wTSWw)SBw(w^TS_Bw)S_Ww = (w^TS_Ww)S_Bw

Notice:

  • $w^TS_W​w$ and $w^TS_Bw$ are scalars, thus we get

αSWw=βSBw\alpha S_Ww = \beta S_Bw

  • If we take $\lambda = \alpha / \beta$ we get $S_B​w=λS_W​w$ which the generalized eigenvalue problem:

SW−1​SB​w=λwS_W^{−1}​S_B​w=λw

From the generalized eigenvalue equation, we derive that the optimal $w$ is:

w∝SW−1(m+−m−)w∝ S_W^{−1}(m_+−m_−)

Yes but how?!

Notice $(m_+​−m_−​)^Tw$ in $S_B​w=(m_+​−m_−​)(m_+​−m_−​)^Tw$ is a scalar. That means the equation looks like $S_B​w=c.(m_+​−m_−​)$. This shows that $S_B​w$ is always proportional to $(m_+−m_−)$ regardless of what $w$ is! Plug this into the equation above to get the generalized eigenvalue equation.

To summarize, Fisher’s Discriminant,

  • Gives the linear function with the maximum ratio of between-class scatter to within-class scatter
  • The problem, e.g. classification, has been reduced from a d-dimensional problem to a more manageable one-dimensional problem.
  • Can be extended to multiclass classification