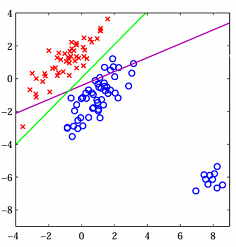
Least-Square Classification
| Type |
|---|
| Linear Classifier |
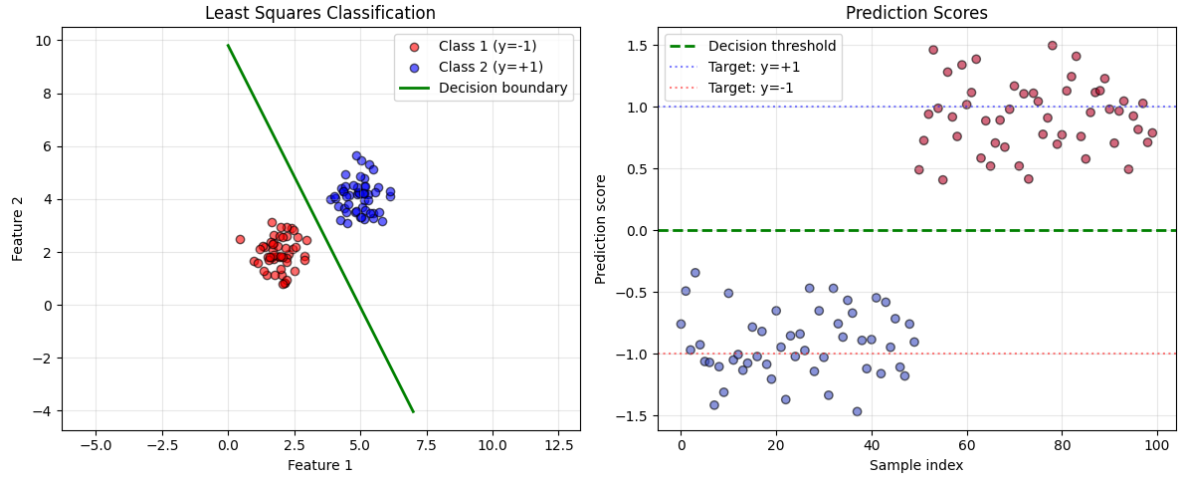
Very similar to linear regression. Same principles apply, just assign {-1, 1} to classes. Then compute the least squares optimization. The decision boundary will always be $f(x)=0$, so the prediction will have a $sign$ function.
2 classes:
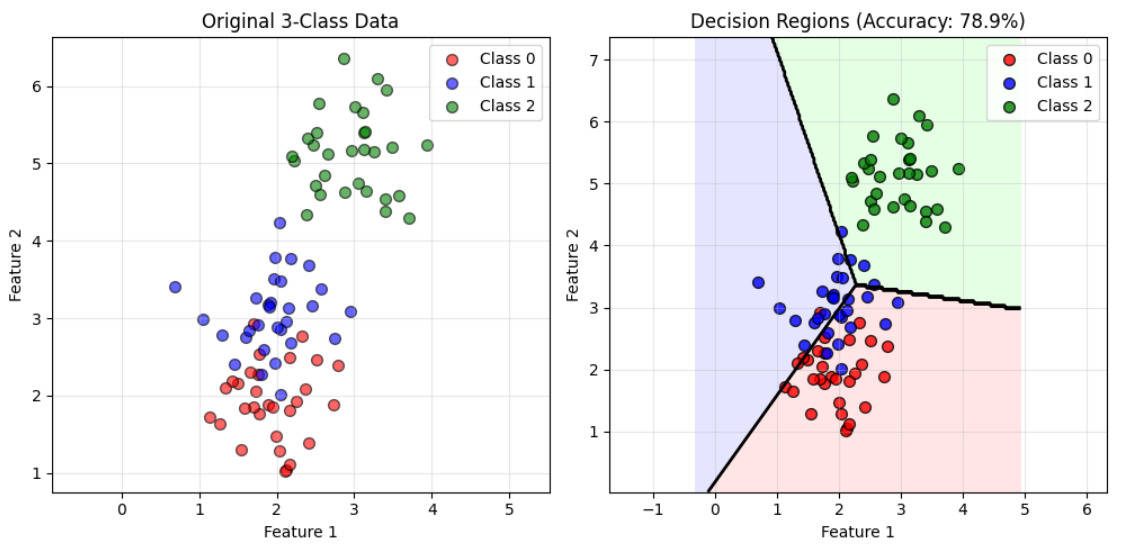
3 classes (example why it might perform badly):
For >2 classes, use one-hot-encoding.
Cons:
- Sensitive to outliers (squared error penalizes large mistakes heavily)
- Not ideal for classification (treats it as regression)
- Can give predictions outside [-1, +1] range
- Often outperformed by logistic regression or SVM
Brain Teaser: You can also try to train two different linear models and try to interpret results.